One challenge for an intelligent interactive tutoring agent is to autonomously determine the difficulty levels of the questions presented to the users. This difficulty adaptation problem can be formulated as a sequential decision making problem which can be solved by Reinforcement learning (RL) methods. However, the cost of taking an action is an important consideration when applying RL in real-time responsive application involving human in the loop. Sample efficient algorithms are therefore critical for such applications, especially when the action space is large. This work (paper). proposes a bootstrapped policy gradient (BPG) framework, which can incorporate prior knowledge into policy gradient to enhance sample efficiency. The core idea is to update the summed probability of a set of related actions rather than a single action at gradient estimation sample. A sufficient condition for unbiased convergence is provided and proved. We apply the BPG to solve the difficulty adaptation problem in a challenging environment with large action space and short horizon, and it achieves fast and unbiased convergence both in theory and in practice. We also generalize BPG to multi-dimensional continuous action domain in general actor-critic reinforcement learning algorithms with no prior knowledge required.
Difficulty Adaptation with Reinforcement Learning
The problem of difficulty adaptation can be formalized using Reinforcement Leanring by taking question difficulty as action and the suitability of a difficulty as reward:
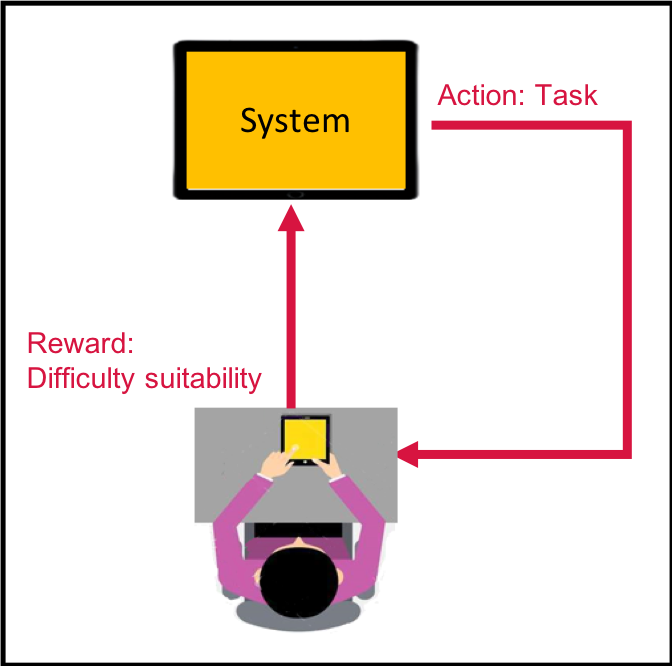
In this way, the difficulty adaptation problem can be solved by reinforcement learning method. One popular reinforcement learning method is policy gradient, which directly takes gradient on the RL objective function. And the gradient can be expressed in an expectation form.
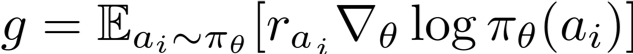
Policy gradient method is considered to be more stable than value-based RL method but a major drawback is its sample inefficiency. Due to the high variance in the gradient estimations, a large batch size is needed to ensure stable policy improvement. In a real-time responsive system, it cannot afford to use large batchsize. In fact, instead of batch update, incremental update with batch size of one is often employed in interactive systems to ensure good user experience. This work investigates how to make policy gradient achieve stable convergence with small batch size.
Bootstrapped Policy Gradient (BPG)
Consider a piece of prior information which states certain actions are likely to have higher/lower reward than others. We will first discuss how to incorporate such prior information into policy gradient with unbiased convergence guarantee and then discuss how such information can be obtained in practice.
What is BPG?
- Bootstrapped Policy Gradient with Better/Worse Actions
The key idea proposed here is to use bootstrap policy gradient with better/worse actions by updating the probability of \textit{a set of actions} instead of a single action in the gradient sample. Specifically, for each action, we defined Better Action Set, which includes the actions that might be better than the current action, and Worse Action Set which contains the worse actions than the current action.

The bootstrapped policy gradient is defined as:
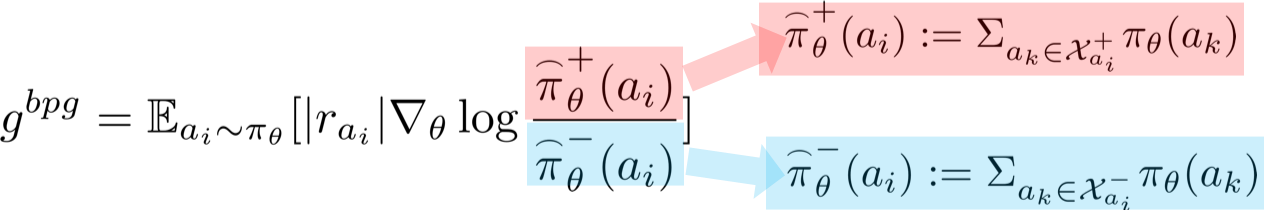
Why BPG?
In the traditional policy gradient, at an individual policy gradient estimation sample, the softmax weight of the sampled action is updated in one direction and all the other actions’ updated in the opposite direction. As a result, the agent is susceptible to being stuck at the sampled action. Specifically, if the sampled action has a better-than-average reward, only the sampled action’s softmax weight will be increased and thus its probability is guaranteed to be enhanced. Hence, the step size needs to be kept very small when receiving positive score function values.
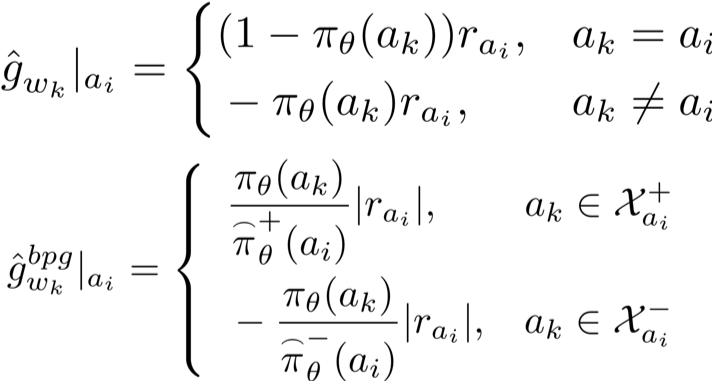
Compared to traditional policy gradient, the proposed method enjoys several advantages. Firstly, in each gradient sample, the agent does not raise a single action’s probability weights but that of a set of actions’. Thus it is more stable and less likely to be stuck with a certain action, regardless of the sign of the reward. As shown in the gradient to the softmax weights, the weight change direction no longer relies on whether the action is the sampled action and the sign of the reward. This property makes it possible for BPG to stably update policy even with the batch size equal to one. Secondly, in BPG the worse action’s probability can be decreased without actually exploring it and the better action’s probability can be increased before it has been selected. It is this property that makes it possible for BPG to find the best action without exhaustively trying every action. In the interactive application, this means that the agent can eliminate some undesirable choices without actually exposing them to the users and use the limited exploration steps to focus on the more promising ones.
How to ensure unbiased convergence?
In spite of the promising properties of the BPG, an immediate question is how to ensure that the surrogate gradient can still lead to the target optimal action, given that the gradient direction has been altered. Notably, the performance of BPG is dependent on the “quality” of the better/worse action set. Therefore, we investigated what kind of constraints on better/worse action set are required for unbiased convergence.
- Equivalent Expression of BPG It turns out that BPG can be expressed in a form similar to the original policy gradient by using a new score function estimator to replace the raw reward.
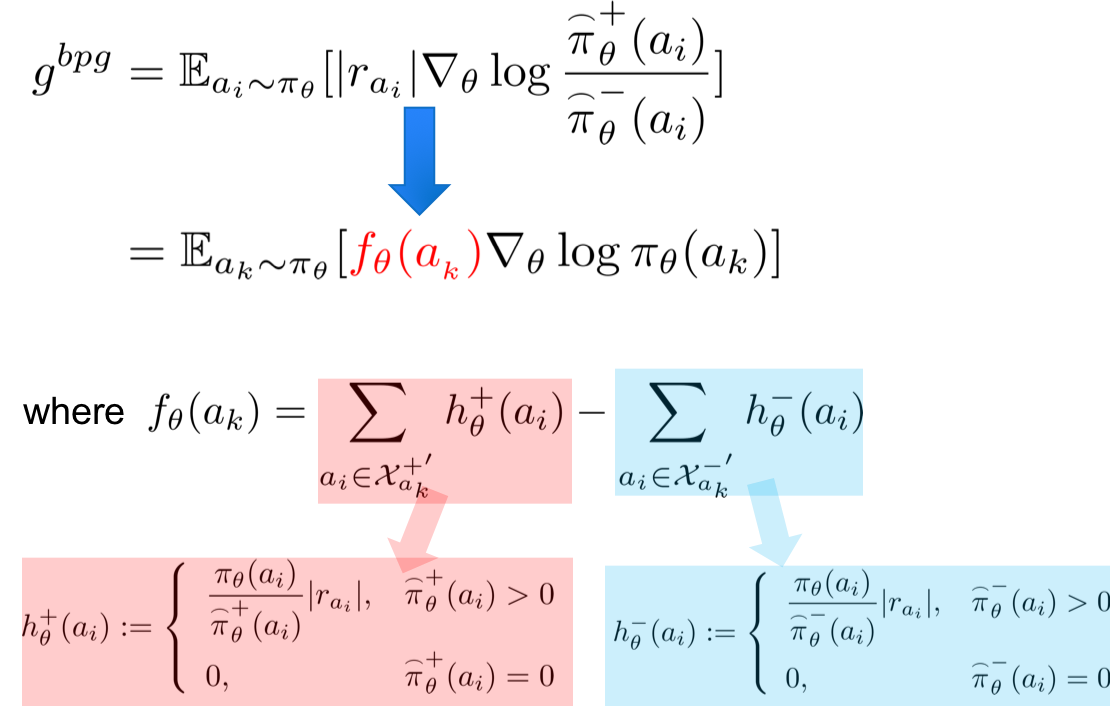
An interesting question is whether there is a certain special class of score function which can make the surrogate gradient direction still converge to the target actions. To answer this question, we provided a surrogate policy gradient theorem.
- Surrogate Policy Gradient Theorem

This theorem points out a class of score function which can guarantee the surrogate gradient to the target action. This class of score function needs to meet two conditions above.
How to obtain Better/Worse Action set in practice?
The remaining questions is how to obtain the prior information of Better/Worse Actions. In the case of difficulty adaptation, there happens to be a convenient way to construct approximate better/worse action sets from prior information of difficulty ranking. Specifically, if a question is observed to be too easy or too hard for the user, then those questions which are even easier or harder than the current one can be considered as worse actions; and in contrast those questions which are harder or easier than the current one can be considered as better actions.

Although the information contained in above better/worse action sets is not accurate, the BPG with these sets can still guarantee unbiased convergence, because the corresponding score function indeed satisfies the sufficient condition. (The proof can be found in the published paper of this work)
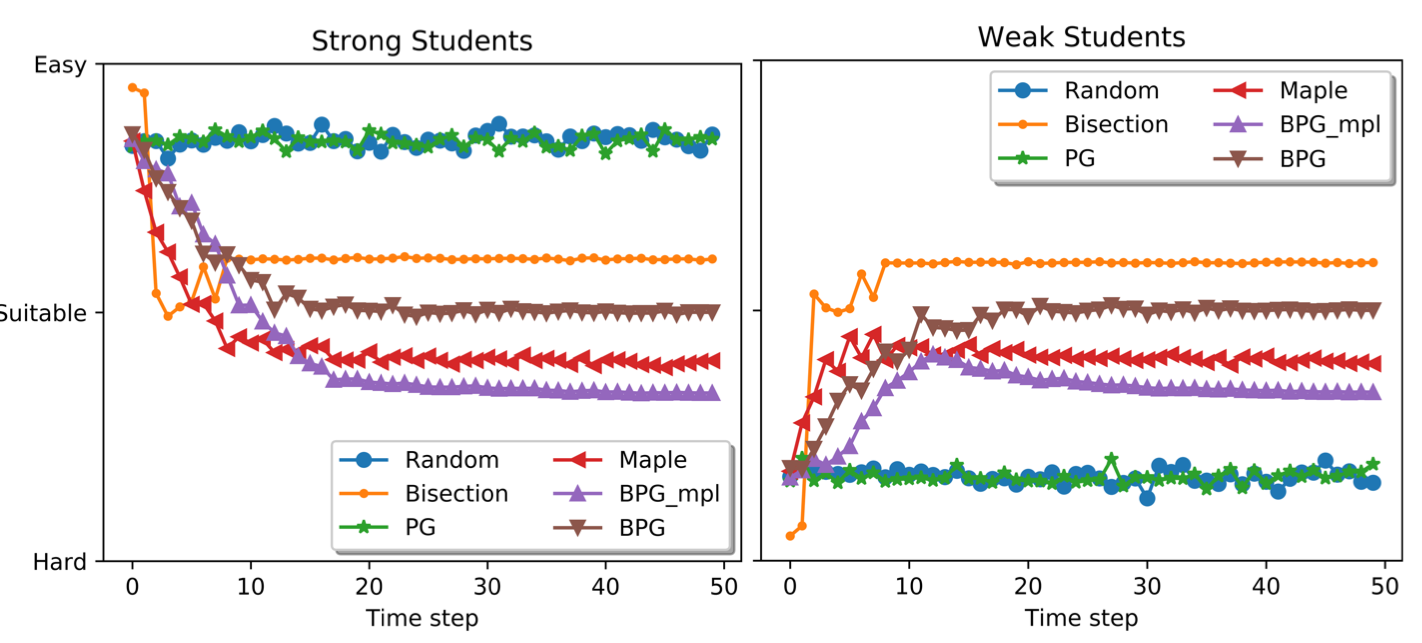
Experimental Results
The proposed difficulty adaptation method is evaluated on simulated data and compared with existing methods. The results showed that only the proposed method achieved unbiased convergence and presented the users with suitable difficulty levels.